2024-10-01
Вопрос: У меня был вопрос о К-факторах для нашего программного обеспечения для 3D-моделирования. Наши инженеры-конструкторы обычно используют коэффициент 0,4 для наших деталей, формованных воздухом. Однако это не очень хорошо работает для наших деталей, которые идут в ручной штамповочный пресс.
Я нашел ваш theArtofPressBrake.com и понял, что помимо этого вопроса, возможно, я мог бы узнать больше. Я хочу помочь нашим инженерам-конструкторам создавать более технологичные детали. Я бы сказал, что у меня хорошее понимание основ, но все еще есть проблемы, с которыми я сталкиваюсь в производственных деталях, которые я откладываю, чтобы иметь в виду для будущих проектов. Можете ли вы ответить на мой вопрос о К-факторах общей рекомендацией, не вдаваясь слишком глубоко в теорию или расчеты?
Ответ: Ответы на ваши вопросы просты; ну, довольно просты. Я начну с основ и дам несколько общих рекомендаций, а затем закончу некоторыми расчетами. Математика лежит в основе гибки листового металла. К счастью, это не слишком сложно — никакого дифференциального исчисления, только геометрия.
Ваш листогибочный пресс и штамповочный пресс формуют листовой металл по-разному. На листогибочном прессе вы производите воздушную формовку, а на штамповочном прессе вы штампуете или чеканите. Это все разные методы формовки, и каждый из них рассчитывается по-разному из-за того, как радиус получается в заготовке.
Сначала давайте сделаем шаг назад и поговорим о типах изгибов, которые можно сделать из листового металла. Не бойтесь; я скоро введу в обсуждение фактор К. До тех пор потерпите.
Существует четыре типа изгибов: минимальный радиус, острый, идеальный и радиусный. Изгиб с минимальным радиусом имеет радиус, равный наименьшему внутреннему радиусу, который можно получить, не сгибая материал. Попробуйте сформировать радиус меньше минимального, и вы сомнете центр радиуса, получив острый изгиб.
Идеальный изгиб имеет радиус, равный или близкий к толщине материала. В частности, радиус идеального изгиба варьируется от минимального значения радиуса до 125 процентов толщины материала. Если ваш радиус составляет 125 процентов толщины материала или больше, у вас радиусный изгиб.
Даже если вы делаете острый изгиб, наименьший радиус, который вы можете использовать для расчетов изгиба, — это минимальный радиус изгиба, если вы хотите, чтобы ваши числа сработали на практике. Обратите внимание также, что воздух, образующий резкий изгиб, обычно очень вреден для однородности. Складка в центре изгиба имеет тенденцию усиливать любые угловые изменения, вызванные изменениями направления волокон материала, твердости, толщины и прочности на разрыв. Чем острее и глубже складка, тем сильнее эффект.
Радиус носика вашего пуансона также играет здесь роль. Если изгиб становится острым на внутреннем радиусе 0,078 дюйма, то радиусы носика пуансона 1/16 дюйма (0,062 дюйма), 1/32 дюйма (0,032 дюйма) и 1/64 дюйма (0,015 дюйма) слишком острые. По мере того, как радиус носика пуансона становится меньше по отношению к толщине материала, тем значительнее будет общее количество угловых изменений, которые вы испытаете.
Есть еще много чего узнать об резких изгибах. Для получения дополнительной информации по этой теме, ссылки на статьи за годы можно найти на моем веб-сайте во вкладке «Медиа» на TheArtofPressBrake.com.
Но я отвлекся. Теперь, когда мы обсудили, какие типы изгибов существуют и как мы их создаем, мы можем перейти к К-фактору. Вы заметите, как разные методы формовки... подождите минутку — мы еще не определили методы формовки: воздушная формовка, гибка дна и чеканка.
И да, между нижней гибкой и чеканкой есть разница. Чеканка заставляет носик пуансона проникать в материал, проникая в нейтральную ось. Дно происходит примерно на 20 процентов выше толщины материала, измеренной от дна штампа. (Примечание: для получения дополнительной информации о методах формовки, включая иллюстрации, см. «Как формируется внутренний радиус изгиба», архив на thefabricator.com.)
Существует большая вероятность того, что комплекты штампов на вашем штамповочном прессе фактически чеканят материал, проталкивая штамп до толщины, меньшей, чем толщина материала. В противном случае вы, вероятно, делаете нижнюю гибку, которая снова происходит примерно на 20 процентов выше толщины материала. Одна заставляет более узкие радиусы, чем другая, но обе заставляют материал достигать определенного радиуса. Независимо от типа вашего изгиба — острый, минимальный, идеальный или радиусный — если вы делаете нижнюю гибку или чеканку, значение носика пуансона определяет результирующий радиус и, следовательно, это то, что мы используем в наших расчетах изгиба.
Однако в воздушной формовке это не так. В воздушной форме полученный радиус — это процент от отверстия матрицы. Изгиб, сформированный в воздухе, плавает по ширине матрицы, а внутренний радиус устанавливается как процент от этой ширины. Процент зависит от предела прочности материала на растяжение. Это называется правилом 20 процентов. Однако это всего лишь название, потому что процент меняется в зависимости от типа материала и предела прочности на растяжение.
Например, нержавеющая сталь 304 образует радиус от 20 до 22 процентов от ширины матрицы, в то время как радиус из алюминия 5052-H32 образует радиус от 13 до 15 процентов от ширины. Общее правило здесь таково: чем мягче материал, тем меньше внутренний радиус.
Кстати, мягкая холоднокатаная сталь 60-KSI является нашим базовым материалом для большинства расчетов, включая правило 20 процентов. Этот материал образует радиус от 15 до 17 процентов от ширины матрицы. Мы начинаем со среднего значения, 16 процентов, а затем корректируем по мере необходимости. Допустим, нам нужно работать с материалом 120-KSI. Это вдвое больше 60 KSI нашего базового материала; следовательно, этот лист 120-KSI будет формоваться воздухом с радиусом, который примерно вдвое больше радиуса мягкой холоднокатаной стали — или 32 процента от отверстия матрицы (16 процентов × 2).
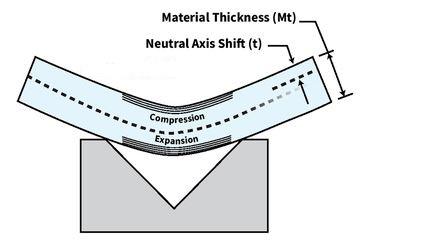
В листовом металле коэффициент К — это отношение нейтральной оси к толщине материала. Когда формируется кусок металла, внутренняя часть изгиба сжимается, а внешняя часть расширяется (см. рисунок 1). Нейтральная ось — это область перехода между сжатием и расширением, где не происходит никаких изменений в материале, за исключением того, что он перемещается из своего первоначального положения на 50 процентах толщины материала к внутренней поверхности изгиба. Нейтральная ось не меняет своей длины, а вместо этого перемещается; это вызывает удлинение во время изгиба. Насколько смещается нейтральная ось, зависит от физических свойств данного материала, его толщины, внутреннего радиуса изгиба и метода формования.
Возьмите обычное значение коэффициента К по умолчанию 0,446, умножьте его на толщину материала, и вы узнаете, куда сместится нейтральная ось. По сути, мы переносим измеренную длину с большего радиуса (то есть длины нейтральной оси на 50 процентах толщины материала) на меньший радиус. Та же общая измеренная длина, распределенная по меньшему радиусу, означает, что у нас есть избыточный материал или удлинение.
Рассмотрим материал толщиной 0,060 дюйма. Умножим это на коэффициент K 0,446, чтобы получить 0,0268 дюйма. Ось сместилась с 0,030 дюйма (при половине толщины материала) до 0,0268 дюйма, если измерять от внутренней поверхности изгиба. Другими словами, ось сместилась на 0,0032 дюйма внутрь. Отсюда мы можем найти ответы, необходимые для наших расчетов изгиба.
Обратите внимание, что тип материала, метод формования и соотношение радиуса изгиба к толщине материала дают нам разные коэффициенты K. Они, в свою очередь, влияют на общую величину удлинения, которое происходит, и на вычеты изгиба, которые нам нужно использовать.
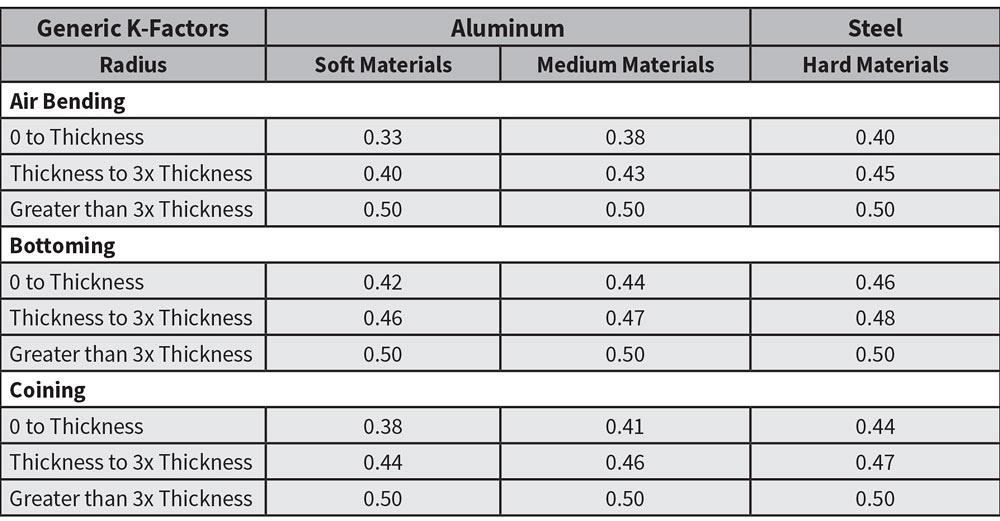
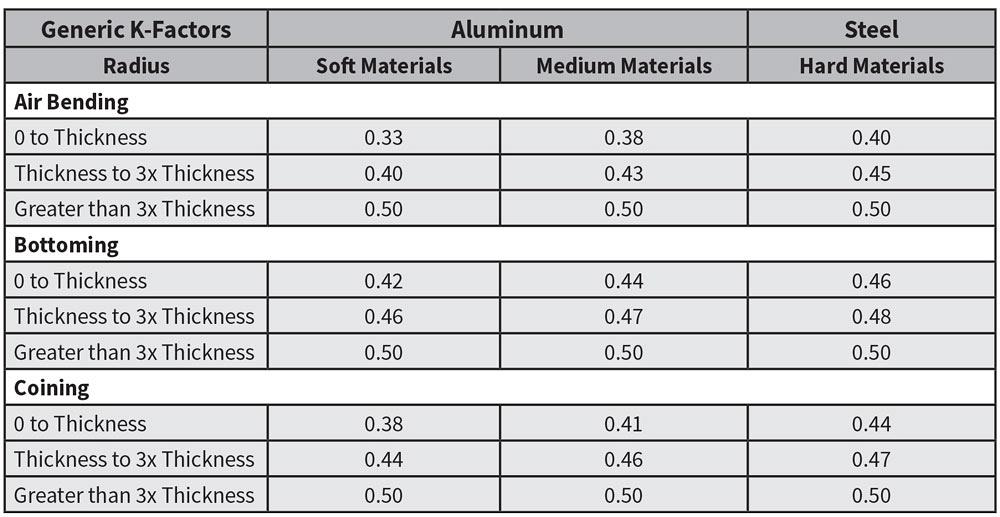
Коэффициент K математически определяется как t/Mt, где t — это положение нейтральной оси, а Mt — толщина материала. Из-за специфических свойств любого данного металла нет простого способа идеально рассчитать это значение, отсюда и диаграмма на рисунке 2.
К-фактор обычно находится где-то между 0,3 и 0,5. Если вы хотите рассчитать К-фактор, а не использовать диаграмму, вам понадобятся несколько тестовых образцов — для этой цели вполне хватит четырех или пяти образцов.
Чтобы рассчитать К-фактор, вам нужно собрать некоторую информацию. Во-первых, вам нужно знать размеры до и после формовки и измерить внутренний радиус как можно точнее. Оптический компаратор является хорошим первым выбором из-за его точности; другие варианты включают калибровочные штифты и радиусные калибры.
Возьмите сумму сформированных внутренних размеров, вычтите плоский размер, и вы получите допуск на изгиб (BA). Затем измерьте дополнительный угол изгиба и внутренний радиус изгиба (Ir). С этими точками данных, а также толщиной материала (Mt), вы можете решить для K-фактора (все размеры указаны в дюймах):
K-фактор = [(180 × BA) /
(π × Дополнительный угол изгиба × Mt)] – (Ir / Mt)
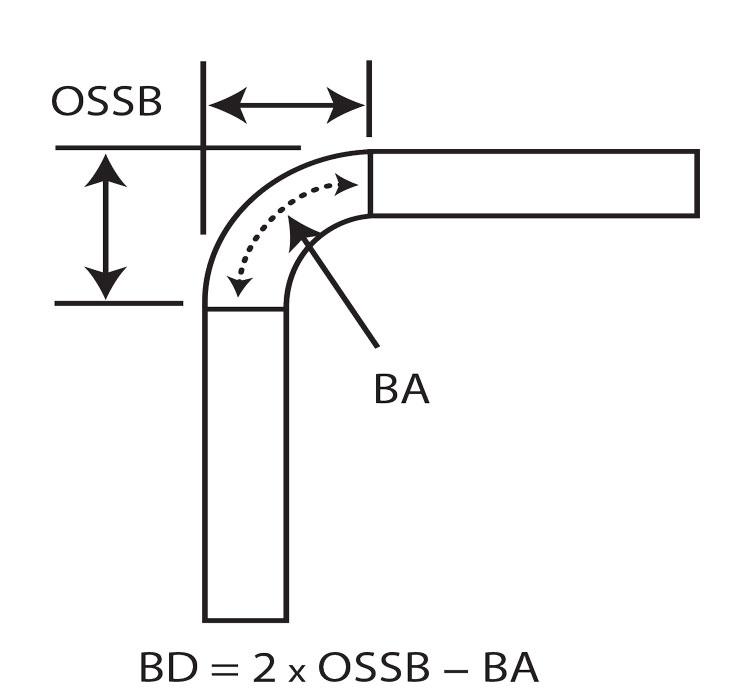
Конечно, проще всего использовать известный K-фактор из таблицы, как на рисунке 2. Вы можете использовать этот K-фактор и внутренний радиус изгиба для расчета нейтральной оси. Затем используйте радиус нейтральной оси для расчета длины дуги нейтральной оси, которая равна вашему BA. Затем вы вычисляете внешний отступ (OSSB), размер, показанный на рисунке 3. Это, вместе с вашим дополнительным углом изгиба (см. рисунок 4), дает вам все, что вам нужно для расчета вычета изгиба (BD) или общего количества удлинения, которое произойдет при данном изгибе:
BA = [(0,017453 × Ir) + (0,0078 × Mt)] ×
Дополнительный угол изгиба
В этом расчете играет роль K-фактор. Вы, вероятно, задаетесь вопросом, что это за числовые значения в формуле — 0,017453 и 0,0078. Что они представляют? Что 0,017453 — это пи, деленное на 180, а 0,0078 — это (π/180) × K-фактор.
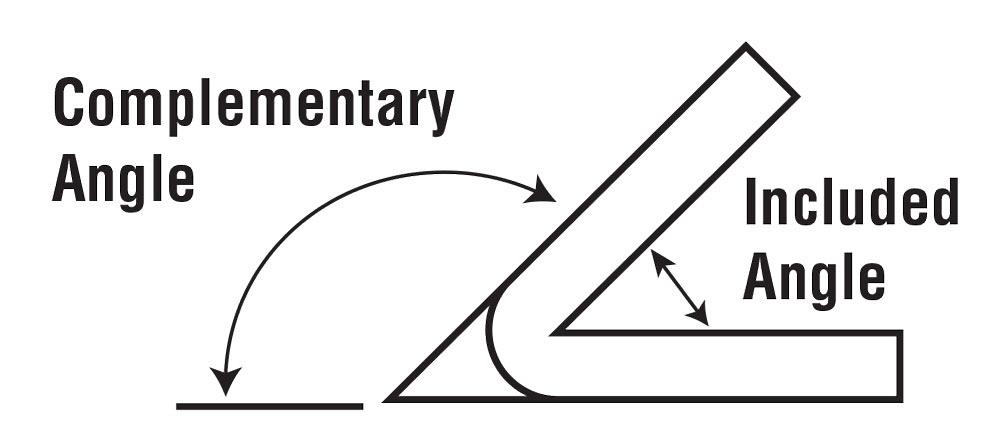
В этой формуле используется коэффициент К 0,446. Тем не менее, если у вас есть какие-либо изменения в методе формовки, типе материала или соотношении внутреннего радиуса изгиба к толщине материала, у вас будет другое значение коэффициента К. Чтобы включить это новое значение, вы можете использовать расширенную версию той же формулы. Затем вы определяете OSSB, а затем используете результат вместе с BA для расчета вычета изгиба:
BA = {[(π/180) × Ir)] + [(π/180) × K-фактор] × Mt}
× Дополнительный угол изгиба
OSSB = [(Tan(угол изгиба/2)] × (Mt + Ir)]
BD = (OSSB × 2) – BA
Используя Y-фактор, ваши расчеты могут быть еще точнее. Однако это требует от вас изменения формулы для BA. Y-фактор учитывает напряжения внутри материала, а K-фактор — нет. Тем не менее, K-фактор все еще участвует, просто немного измененный.
Чтобы найти Y-фактор, вы можете обратиться к таблице (см. Рисунок 5) или использовать это уравнение:
Y-фактор = (K-фактор × π)/2
Затем мы вставляем Y-фактор в новую формулу для BA: BA = {[(π/2 ) × Ir ] + (Y-фактор × Mt )}
× (Дополнительный угол изгиба/90)
Мы рассмотрим процесс для обоих наборов уравнений, используя мягкую холоднокатаную сталь 60-KSI толщиной 0,062 дюйма с внутренним радиусом изгиба 0,062 дюйма и углом изгиба 90 градусов. Для этого примера мы будем использовать K-фактор 0,446.
Y-фактор = (0,446 × π)/2 = 0,7005
BA = {[(π/2 ) × 0,062)] + (0,7005 × 0,062)}× (90 / 90) = 0,1408
OSSB = [(Tan(90/2)] × (0,062 + 0,062)] = 0,124
BD = (0,124 × 2) – 0,1408 = 0,1072
Теперь вот расчеты изгиба с использованием только K-фактора и нашего исходного уравнения BA: BA = {[(π/180) × Ir)] + [(π/180) × K-фактор] × Mt} × Дополнительный угол изгиба
BA = [(0,017453 × 0,062 ) + (0,0078 × 0,062)] × 90 = 0,1409
OSSB = [(Tan(90/2)] × (0,062 + 0,062)] = 0,124
BD = (0,124 × 2) – 0,1409 = 0,1071
Разница в BA между двумя расчетами составляет всего 0,0001 дюйма, а разница в BD также составляет 0,0001 дюйма, что в этом примере делает эти два способа расчета BA функционально одинаковыми. Но измените угол изгиба или внутренний радиус изгиба, и все изменится. Вы обнаружите, что последний набор формул с использованием Y-фактора немного точнее, чем с использованием K-фактора.
В отрасли принято использовать значение 0,446 для значения K-фактора. Но, выбрав правильные значения данных, включая K-фактор на основе переменных, специфичных для конкретного применения (тип материала, метод формовки и внутренний радиус), я думаю, вы обнаружите, что многие проблемы, с которыми вы сталкиваетесь между двумя различными методами производства, исчезнут.
Стив Бенсон является членом и бывшим председателем Совета по технологиям прецизионной листовой обработки Международной ассоциации производителей и производителей. Он является президентом ASMA LLC, steve@theartofpressbrake.com. Бенсон также проводит Программу сертификации FMA по прецизионному гибочному прессу, которая проводится по всей стране. Для получения дополнительной информации посетите сайт www.fmanet.org/training или позвоните по телефону 888-394-4362. Последняя книга автора, Bending Basics, теперь доступна в книжном магазине FMA, www.fmanet.org/store.
Предлагаем гибочный инструмент： пуансоны и матрицы для гибочных прессов с различными системами крепления, таких как: Amada Promecam, Aliko, Yawei, Durmazlar, Baykal, Accurl, Accurpress, LVD, Darley, Насо, Wila, Trumpf, Rolleri, UKB, Eurostamp и тд.
Статья воспроизведена с：https://www.thefabricator.com/thefabricator/article/bending/k-factors-y-factors-and-press-brake-bending-precision
