2024-10-21
Факторы, влияющие на точность расчетов гибки на листогибочном прессе
Вопрос: В настоящее время я использую листогибочный пресс, который вычисляет плоскую длину материала перед его изгибом, но, похоже, он не подчиняется ни одной из формул допуска на изгиб, которые я где-либо видел.
Например, я обычно гну листы толщиной 0,67 мм с помощью матрицы 12 мм и пуансона с радиусом 1 мм. Для изгиба на 90 градусов машина вычисляет, что мне нужно отнять 1,54 мм от исходного материала, учитывая тот факт, что он имеет размер снаружи. Учитывая наш инструмент, мы должны получить внутренний радиус 1,872 мм. Но когда я вставляю это в наши формулы изгиба, результирующий вычет изгиба оказывается даже близко не таким, как 1,54 мм, как говорит машина.
Было бы здорово, если бы вы могли дать мне несколько указаний относительно того, почему машина, похоже, запрограммирована с другой формулой, чем все те, о которых я читал. Также извините за метрические измерения; я из Великобритании.
Ответ: Не беспокойтесь о метрических измерениях; мы работаем как с метрическими, так и с имперскими единицами здесь, в штатах. Сказав это, давайте посмотрим, сможем ли мы решить эту проблему.
Во-первых, отказ от ответственности: не находясь там и не работая с вашим листогибочным прессом и его контроллером, трудно с уверенностью сказать, почему вы находите то, что находите. Кроме того, поскольку я не знаю вашего целевого внутреннего радиуса изгиба, я предположу, что он составляет 1,0 мм (0,039 дюйма). Я также предположу, что ваш угол изгиба составляет 90 градусов, и что вы используете пневматическую формовку с использованием прецизионно шлифованного инструмента.
Итак, почему ваш станок, похоже, использует другую формулу, чем те, о которых вы читали? Хотя многие контроллеры листогибочных прессов используют алгоритмы, которые немного отличаются, они не сильно отличаются от того, что я собираюсь описать. В США эти формулы также можно найти в Machinery’s Handbook.
Существует распространенная путаница в отношении терминов и их применения, а также связанных с ними проблем выбора инструмента, которые следует решить. Эти проблемы возвращают нас к вашему вопросу о данных от контроллера листогибочного пресса.
Большинство контроллеров выполняют свои расчеты на основе некоторых основных параметров, таких как правильный выбор инструмента. Современные контроллеры обычно основывают расчеты, используя метод воздушной формовки, поэтому если вы сгибаете снизу, возвращаемые значения будут неверными.
Программы также не учитывают проблемы, вызванные использованием слишком большого или слишком маленького отверстия матрицы или слишком острым радиусом носика пуансона. Существует также вероятность того, что информация, выдаваемая контроллером, используется неправильно; например, используется ли допуск на изгиб там, где должно быть значение вычета на изгиб?
Начнем с определения формул для трех основных функций изгиба и их применения (см. рисунок 1): внешний отступ (OSSB), допуск на изгиб (BA) и вычет изгиба (BD).
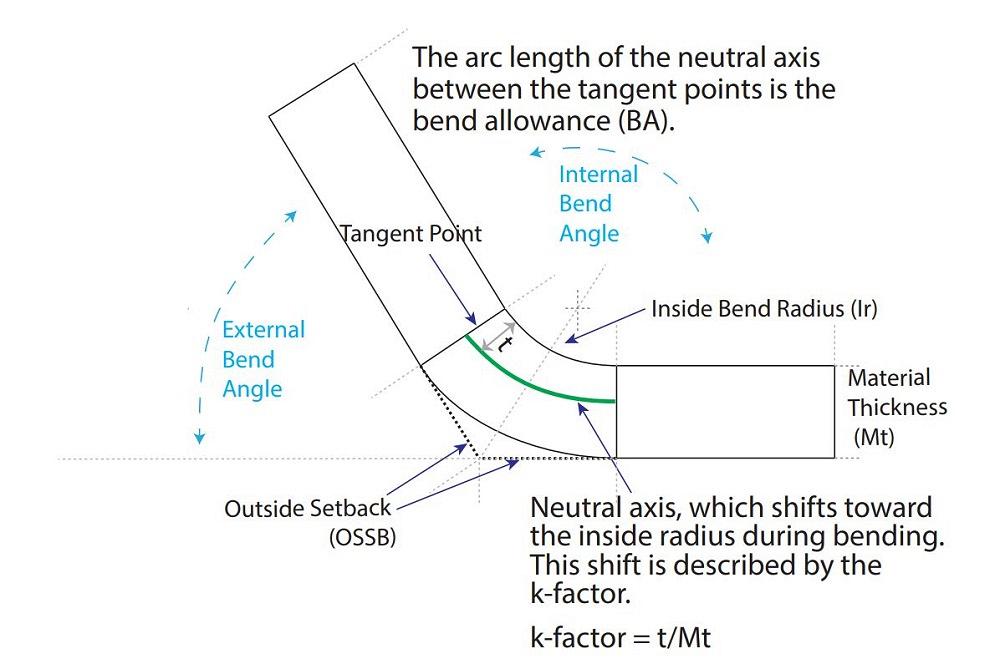
BA – это значение, добавленное к размерам изгиба от края детали до точки касания между плоскостью и радиусом. Оно рассчитывается следующим образом:
BA = [(0,017453 × Внутренний радиус изгиба) + (0,0078 × Толщина материала)] × Внешний угол изгиба
Обратите внимание, что значение 0,017453 равно pi, деленному на 180. Это значение 0,0078 получается путем умножения 0,017453 (опять же, pi, деленное на 180) на k-фактор. В этом случае k-фактор равен 0,4468. Кроме того, угол изгиба всегда указывается как измерение внешнего угла (то есть внешний угол изгиба на рисунке 1).
В вашем приложении BA с использованием имперских единиц измерения будет:
[(0,017453 × 0,039) + (0,0078 × 0,026)] × 90 = 0,0795 дюйма.
Вот та же формула с использованием метрических единиц измерения:
[(0,017453 × 1,0) + (0,0078 × 0,67)] × 90 = 2,0411 мм
Обратите внимание, что при сравнении метрических и дюймовых значений расчеты будут отличаться лишь незначительно:
0,0795 дюйма = 1,981 мм
2,0411 мм = 0,080 дюйма.
Внешний отступ (OSSB) – это измеренное расстояние от радиуса и точки плоской касательной до вершины изгиба:
OSSB = [Tan (половина угла изгиба) × (толщина материала + внутренний радиус изгиба)
Таким образом, для вашего приложения мы рассчитаем OSSB следующим образом:
OSSB в дюймах = [Tan(45)] × (0,026 + 0,039) = 0,065 дюйма
OSSB в миллиметрах = [Tan(45)] × (1,00 + 0,67) = 1,67 мм
Наконец, вы рассчитаете BD следующим образом:
BD = (2 × OSSB) – BA
BD в дюймах = (2 × 0,065) – 0,0795 = 0,051 дюйма
BD в миллиметрах = (2 × 1,67) – 2,041 = 1,299 мм
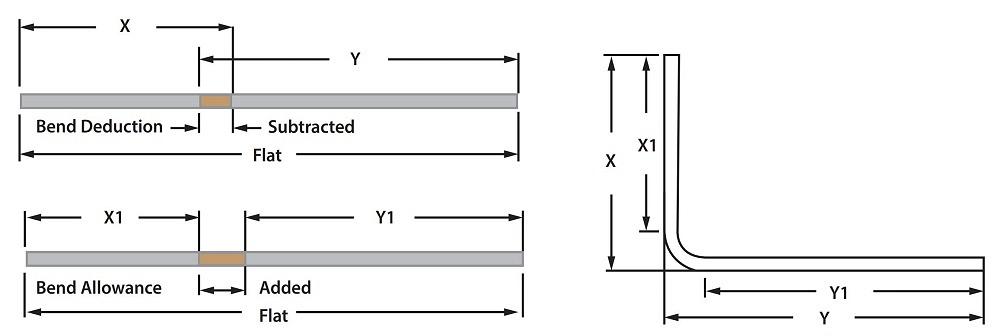
Теперь, когда мы определили формулы и рассчитали некоторые данные, давайте применим эту информацию к плоской заготовке. На рисунке 2 показаны различия между BA и BD. Мы добавляем BA к сумме длин плоскостей от края до точки касания радиуса изгиба; на рисунке это X1 + Y1 + BA. И наоборот, мы вычитаем BD из суммы внешних размеров от края до внешней стороны изгиба. На рисунке это (X + Y) – BD.
Если инженеры или дизайнеры совершают простую ошибку, вычитая BA, когда ее следовало бы добавить, то плоскость будет неправильной. Еще одна распространенная ошибка – использование неправильного метода гибки в расчетах. Например, если вы гибите снизу, вы штампуете радиус носика пуансона в материале. Если вы делаете воздушную формовку, радиус формируется как процент от отверстия матрицы. Если у вас неправильный метод формовки, вы запустите расчеты изгиба с неправильным радиусом, что, в свою очередь, сведет на нет все остальное.
Если вы постоянный читатель моей колонки, вы должны знать важность внутреннего радиуса изгиба. Это сердце гибки листового металла. Если мы ошибемся, почти ничего не получится. Поэтому, если цифры не работают, проверьте внутренний радиус изгиба. Как вы подтверждаете, что он правильный? Вы используете радиусные калибры или штифтовые калибры? Или, если на то пошло, один инструмент лучше другого?
Использование радиусных калибров нормально, когда вы гибите снизу. Радиусы носика пуансона бывают стандартных метрических и имперских размеров. И, поскольку вы гибите снизу, радиус на пуансоне штампуется в материале.
Если вы снова занимаетесь воздушной формовкой, внутренний радиус изгиба плавает как процент от отверстия матрицы. Это означает, что ваш внутренний радиус будет отличаться от стандартных приращений инструмента; полученный радиус редко попадает на общие значения фиксированного инструмента, что делает радиусные калибры непрактичными. Вот где в игру вступают магазинные или контрольные калибры. Поскольку калибры имеют шаг 1 мм или 0,001 дюйма, любой внутренний радиус можно точно проверить независимо от метода формовки.
Просматривая ваши данные, я должен задаться вопросом, почему вы используете такое большое отверстие матрицы для такого тонкого материала. Если вы занимаетесь формовкой воздухом, что, как я предполагаю, так и есть, то ваш внутренний радиус изгиба разрабатывается как процент от отверстия матрицы.
Например, сталь A36 с пределом прочности на разрыв 60 000 фунтов на кв. дюйм должна давать внутренний радиус изгиба, который составляет около 16% от отверстия матрицы. Таким образом, для отверстия матрицы 12 мм (0,472 дюйма) внутренний радиус изгиба должен быть 1,92 мм (0,075 дюйма) – и 1,92 мм очень близко к 1,872 мм (0,073 дюйма), которые вы рассчитали.
Расчет вашего станка 1,54 мм (0,060 дюйма) является правильным BD для внутреннего радиуса изгиба 1,803 мм (0,071 дюйма) – близко к радиусу 1,872 мм, который вы рассчитали, но не является точным совпадением. Почему? Конечно, возможны небольшие вариации в уравнениях, например, вариация k-факторов, на что есть веские причины.
Но если полученный радиус изгиба отличается от того, что рассчитали вы или машина, причиной может быть вариация материала. Как я уже много раз обсуждал ранее, нет двух одинаковых кусков материала, даже если они обозначены как имеющие одинаковую марку материала, толщину, предел текучести и прочность на разрыв и даже сформированные вдоль одного и того же направления волокон.
Изменчивость материала также может влиять на правило 20%. Названное в честь характеристик формовки нержавеющей стали воздухом, правило 20% – это то, откуда берется это значение 16%. Тем не менее, правило не является точным, но вместо этого имеет диапазон значений, которые мы могли бы использовать. Материал A36, который я выбрал для этого примера, имеет значения в диапазоне от 15% до 17% от отверстия матрицы. Это, опять же, происходит из-за различий в формуемом материале. Иногда разброс значений может быть еще больше. Тем не менее, медианное значение обычно очень точное.
Опять же, не находясь там и не работая с вашим листогибочным прессом и его контроллером, трудно дать вам точный ответ на вопрос, почему ваш контроллер делает то, что он делает. Независимо от этого, я надеюсь, что предложил некоторую базовую справочную информацию, показал вам, как ее применять, дал вам некоторые идеи о том, почему вы видите те результаты, которые видите, и что вы можете сделать, чтобы исправить это.
Помните, всякий раз, когда вы не можете понять проблему, продолжайте пытаться; вы поймете. Такие проблемы могут превратиться в отличный опыт обучения.
Статья перепечатана из:https:
https://www.thefabricator.com/thefabricator/article/bending/press-brake-controllers-and-the-bend-deduction-of-sheet-metal
Предлагаем гибочный инструмент: пуансоны и матрицы для гибочных прессов с различными системами крепления, таких как: Amada Promecam, Aliko, Yawei, Durmazlar, Baykal, Accurl, Accurpress, LVD, Darley, Насо, Wila, Trumpf, Rolleri, UKB, Eurostamp и тд.